RENT A THINKER
Home			My Page	Chat			Tik-Tok

5        A DSP based Low Precision Algorithm for Neural Network using Dynamic Neuron Activation function.

5.1       Abstract
5.2       Introduction: 
5.3       Proposed Algorithm: 
5.4       Training  
5.5       Results 
5.6       Conclusion  
5.7       References 
5.8       Appendix-1 
5.9       Published 

5.1       Abstract 

Most of the neural network applications are based on computer simulation of back prorogation  (BP). The BP algorithm uses floating-point arithmetic which is computational intensive and hence slow on small machines. An integer algorithm similar to BP algorithm is developed, which is suitable for DSP (Digital Signal Processor) devices and micro controllers. The algorithm uses integer neuron activation function with bounded output.  The training of the network involves the training or the modification of the activation function coefficients. This results in reliable convergence of error with increased speed and less local minima problems.  Using this algorithm, the error convergence rate is found better than the conventional B.P algorithm for analog and digital problems. This algorithm is implemented on DSP based neural hardware.

 Algorithm: For analog and digital problems. This new algorithm is implemented on DSP based neural hardware.

 Keywords:  Multi Layer Perceptron (MLP), Back Propagation Learning, Activation function, DSP, Micro Controllers.  

5.2       Introduction:  

Multi layer neural networks are increasingly being used in solving industrial problems like fault diagnostic, sensor data fusion, optimization, process modeling etc. Most applications use multi-layered networks on PCs and work stations with Back Propagation (BP), which uses floating-point computations. However many applications demand the use of small computers to run neural network programs like sensor data fusion, fault diagnostics etc. Although DSP have limited memory space and limited arithmetic capabilities, they are most suitable for these applications.  The earlier work done by the author in this field [4] is based on stochastic algorithm, which runs on micro controllers with small size code and runs without multiplication and division operation.  However the stochastic algorithm is limited to binary input-output neurons operation.  For analog representation of each input variable, a number of input neurons are required in a binary coded form. The use of the integer arithmetic with intrinsic instruction codes can give better execution speed. 

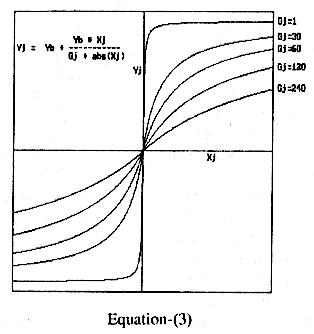
An algorithm can be developed to train multi layer neural network with analog input using low precision integer arithmetic. The exponential sigmoid function used in conventional BP is simplified. The activation function developed of the form - 

 Yn = Yb + Yb * Xn / (Gn + abs (Xn))................(1) 

where  Xn is the analog input in the range of -2¹⁵ to +2¹⁵. Yb is the offset and it is half the maximum value of Yn. Gn is a variable here, which decides the slope of the activation function. The value of Gn is dynamically adopted during reinforcement of the weights. This optimizes the learning. To reinforce the weights, the first derivative of activation function is used in B.P algorithm. However, the equation-1 is not differentiable at Xn=0.  Hence the reverse characteristics is approximated to the form- 

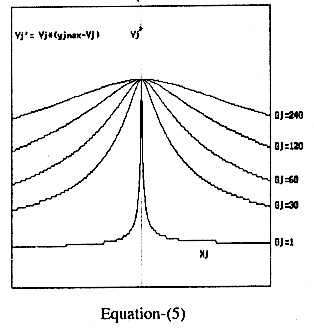
 Yn' = Yn * (Ynmax - Yn)............................(2)_ 

Equation-2 is similar to the first derivative of the popularly used sigmoid function-

Yn = 1 / 1+e^-xn.  

Activation function 1 and 2 are shown in figure-1. The activation function -2 is a bell shaped curve having maximum at Xn=0. This curve can be considered as curve of willingness to learn.  As seen from the plot the network is more receptive to learn near Xn=0 and will have stable memory or be less likely to forget at high values of Xn. The lower value of Xn may be considered as a childhood condition where learning process is fast. At the higher values of Xn, the behavior of the network becomes adult, where the network does not forget easily. It is found that the forward and reverse characteristics could be chosen independently as long as the above criterion is maintained. In this algorithm, activation function and its reverse characteristics Yn' are not related. However, the characteristics of the activation function should be kept similar. 

5.3       Proposed Algorithm: 

The proposed algorithm is similar to BP algorithm, except the reverse characteristic of the neuron is not derived from the forward characteristics of the activation function. Let us consider a multi layer network with three layers i, j and k. The Xi, Xj, Xk and Yi, Yj, Yk are the inputs and outputs of the neurons at layers I, j and k respectively. Wji and Wkj are the weights between the I-j and j-k layers. 

During the forward pass, using equation-1 we calculate the value of Yj as follows-  

Yj = Yb + Yb * Xk / (Gj + abs (Xj))...............(3)

where  Xj =  åYi * Wji + Wjb...............(4) 

In the reverse pass using equation-2 we calculate the value of Yj’ as follows-

Yj’=Yj * (Yjmax – Yj) ……………(5) 

In equations 3, 4 and 5,  Xj, Wji and Wjb are 16 bit integers and Yj is 8 bit short integer. The Wjbs are the bias weights. Yb is chosen to be 128, which is half of the dynamic range of Yj. Gj is a coefficient of activation function. The output range of Yk is same as Yi and Yj (i.e. 8 bit short integer). 

 Fig-1 Plot of proposed activation function with different values of Gj.  

5.4       Training  

We consider the error function as-  

E = ½å(Yk - dk)²  ..…….(6) 

where dk is the desired output in the range of 0 to 255. The reinforcement of coefficients of the activation function (Gk and Gj) in multi layer Neural Network is achieved by calculating the sensitivity of activation function coefficient (AFC) with respect to the error function.  This allows the network to adopt the most appropriate function for a given iteration (trial). Fig-2 shows the plot of AFC for hidden and output neurons. The diagram shows both Gj and Gk starts at 50 and finally stabilizes at 100 and 1 respectively. It is seen that the value of AFC is different for different layers. Hidden layer adopts a large value of coefficient keeping the slope low.  

The weights Wkjs are reinforced using - 

wkj [k][j] = wkj [k][j] - r*yj[j]/eta.....(7) 

Gk = Gk - r * yk[k]/eta.....(8) 

where r = (yk[k]-out[k]) * yk[k] * (256-yk[k]) .....(9) 

wji[j][i] = wji[j][i] - s * yi[i] /eta.....(10) 

Gj= Gj - s*Xj[j]/eta.....(11) 

where s = y_j[j] * (256-y_j[j]) * å{(y_k[k]-out[k])*y_k[k] * (256-y_k[k])* w_kj[k][j]}....(12) 

In the above expressions Gk, Gj, Yk, Yj and 'eta' are unsigned integers and all others terms signed integers. In the actual implementation, the factor ‘eta’ is implemented after every multiplication to scale down the product, in order to avoid the overflow. Appendix-1 shows a C-code implementation for the ADSP-2105 DSP device. 

5.5       Results 

The algorithm is tested using digital and analog input output functions with different types of network topology. Table - 1 shows the comparison of digital input output learning for different configuration using XOR function with conventional BP algorithm. The network column, the number (4-4-2) represents number of input neurons, hidden neurons and output neurons. The input output used is binary and function XOR. The algorithm is also tested using analog input output. Table-2 shows the comparison of digital input output learning for different configuration using Non linear function like circular boundary with conventional BP algorithm.  In Table-2, in network column, the number (2-10-1) represents number of input neurons, hidden neurons and output neurons. The input output used is binary and function is non-linear boundary mapping. Fig-3 shows the output of a network consisting of two analog inputs, which is used to map a circular boundary in 128 x 128 image frame. The network has 2 analog input neurons, 12 hidden neurons and 1 binary output neuron. The output is 1 when Xi[0]²+Xi[1]² is less then (radius)².

Table 1: Comparison of Conventional BP and proposed integer algorithm. 

 Table-1 compares the conventional BP algorithm with proposed algorithm. In the network column, the number (4-4-2) represents number of input neurons, hidden neurons and output neurons. The input-output used is binary and function is XOR.  

 Table-2 compares the conventional BP algorithm with proposed algorithm. In the network column, the number (2-10-1) represents number of input neurons, hidden

neurons and output neurons. The input-output used is binary and function is non-linear boundary prediction. 

5.6       Conclusion 

A   Low precision integer arithmetic algorithm for multi layer feed forward networks has following main features: 

(1) The conventional B.P algorithm needs high floating-point computation and hence is very slow on small machines. The low precision algorithm with integer neuron activation function with bounded output is comparatively simple in operation and offers higher speed. 

(2) The proposed algorithm involves the training or the modification of the activation function coefficients (AFC).  

(3 The error convergence rate is found much better than the conventional BP algorithm for analog and digital problem. 

5.7       References 

[1] Lippmann R.P., An introduction to computing with Neural Nets. IEEE ASSP Magazine, pp4-22, April, 1987. 

[2] D.E. Rumelhart and J.L. McClelland, Parallel Distributed Processing: Explorations in the Micro structure of Cognition. Cambridge MA:MIT Press, vol. 1,1986. 

[3] R. Hetcht-Nielsen, "Theory of the back propagation neural network," in Proc. Int. Joint Conf. Neural Networks, vol.1, pp.593-611. New York: IEEE Press, June 1989. 

[4] H. S. Mazumdar, " A multi-layered feed forward neural network suitable for VLSI implementation", International journal : Micro controllers and Micro system, Volume-19, Number-4, pg-132-234, May, 1995.

5.8       Appendix-1 

/*******************************************************
* A low precision Algorithm for Multi layer            *
* Feed Forward Neural Network                           *
* by Himanshu Mazumdar                                      *   
********************************************************/
# define KKM 128    /* maximum output neurons*/
# define JJM 128    /* maximum hidden neurons */
# define IIM 128   /* maximum input neurons  */  

/* Definition of Global Variables  */
int out  [KKM] ;   /* Expected Output*/
int yk   [KKM] ;   /* Output of output neuron*/
int xk   [KKM] ;   /* Input to output neuron*/
int yj   [JJM+1];  /* Output of hidden neuron*/
int xj   [JJM] ;   /* Input to hidden neuron*/
int yi   [IIM+1];  /* Input to the network */
int wkj  [KKM][JJM+1];/* Weights connecting hidden to output neurons*/
int wji  [JJM] [IIM+1] ;  /*Weights connecting input to hidden neurons*/
int Gj=100,Gk=100;   /*Constant related to the slope of curve of activation function */
int ii,jj,kk;
/***************** Training ******************/
void Training(void)
{
 int i,j,k;
 long r,s;
 for ( k=0; k<kk;  k++ ){
 /* Output layer weights and Gk update*/
 r = (long)(yk[k]-(int)out[k]) * yk[k] * (256- yk[k]);
 r = ashift(r,13); /* Divided by 2_13_ */
 for ( j=0; j<jj+1; j++ ){
 wkj[k][j] -= ashift(r *yj[j],11); /* update wkj */
 r = - (long)(yk[k]-(int)out[k])*yk[k]*(256-yk[k])*xk[k];
  /* reinforcement of Gk*/
 if(r>0) { if(Gk>1)Gk--;}
   else{if(Gk<100)Gk++; }
 }}
 for ( j=0; j<jj; j++ ){
 /* hidden layer weights and Gj update */
 r=0;
 for ( k=0; k<kk;  k++ ){
 s=(long)(yk[k]-out[k]) * (long)yk[k] * (long)(256-yk[k]);
 s=ashift(s,13);  /* Divided by 213 */
 r += s * wkj[k][j];}
 r = ashift(r,6);  s=-r*Gj*xj[j];
 if (s>0) {if(Gj>1) Gj--;}
   else  { if(Gj<100) Gj++; } /* Gj update */
 r =r* yj[j] * (256-yj[j]);            
 r=ashift(r,13); /* Divided by 2_13_ */
   for ( i=0; i<ii+1; i++ ){ 
        wji[j][i] -=ashift( r * yi[i],10); }
              /* wji update */
     }
}
 /************ Signed Arithmetic shift ****************/
long ashift(long dt,int sft)
{
  unsigned i;
   if (dt>=0) dt=dt>>sft; else {dt=-dt; dt=dt>>sft; dt=-dt;}
   return(dt);
}
/*********************************************************/

5.9   Published

Mazumdar Himanshu S. and Rawal Leena P.,   "A DSP based Low Precision Algorithm for Neural Network using  Dynamic Neuron Activation Function", CSI (Computer Society of India) Communications, April (pp. 15 - 18), 1996, INDIA.