RENT A THINKER
Home My Page Chat Tik-Tok
7        A Neural Network Tool Box using C++

7.1       Abstract
7.2       Introduction  
7.3       On Tool Box Implementation  
7.3.1        Neural Net Designer-1 (For Feed Forward Type Network)
7.3.2        Neural Net Designer-2 (For Feed Back Type Network)
7.3.3        Neural Net Designer-3 (For Unsupervised Learning)
7.4       Proposed Algorithm for Pruning  
7.5       Results 
7.6       Conclusion  
7.7       References 
6.14     PUBLISHED 

 

7.1       Abstract 

            An interactive Neural Network developing Tool Box is designed using C++. The Neural Networks are emerging computational technique used for artificial intelligence applications. Neural Networks are used for speech and image recognition, feature extraction, and associative memory applications. For simulation of Neural Network OOPs (Object Oriented Programming) are found most suitable programming language. The paper describes in general the Neural Network optimizing algorithms used in above implementation illustrated with results. 

7.2       Introduction 

Artificial Neural Network (ANN) is a problem solving technique, which tends to simulate the natural system of brain. ANN is in far too primitive stage compared to the brain of lowest biological species. This is mostly because of the complexities of the biological systems. ANNs are inherently parallel processing technique. Increase of processing power is almost proportional to the number of processing elements in an ANN system. There are two important characteristics of ANN systems: 

  1. Similar processing is performed in large number of data sets.
  2. Different operations are performed on same data set.

In multilayer type network, there are similarities of the data structures of different layers. Also there are different processes like network updating, network weight reinforcement, network monitoring, network loading and network saving etc. which work on same data set. These two properties of ANN are also the important properties of object oriented programming languages. Data hiding is another important aspect of OOP, which is relevant to ANN implementation. In ANN the certain data structures are associated with specific operations only. For example, the delay time of delay neurons or the address map of random interconnections are processed by certain objects or friendly objects only. OOP hides the complexities of data structure from the higher-level programming. Considering the features of OOP and ANN, a general-purpose toolbox is designed using Borland C++. 

This toolbox consists of three packages. These packages are: “Neural Net Designer Part I, II and III for Feed Forward type multi layer networks, feedback type networks and for self learning type neural networks respectively”. Brief overview of these packages with the details of the aspects like network configuration and network optimization is given below.  

7.3       On Tool Box Implementation 

The packages are designed in three parts. In all the packages, a self contained integrated environment is created based on interactive window to develop Neural Network type applications with online graphics display. The systems have following main features. The packages are dedicated for Feed Forward, Feed Back, and Unsupervised learning. 

7.3.1     Neural Net Designer-1 (For Feed Forward Type Network) 

·        Interactive and user friendly window

·        Real time graphics display

·        Network view

·        User definable and standard neuron activation functions and summing functions

·        Flexible connectivity, layered and random connections

·        Learning and forgetting coefficients

·        Optimizing of network

·        Graphics and numeric data generation support

·        Run time probing of neurons

·        Time series prediction using delay neurons

·        Image band compression using feature extraction 

7.3.2     Neural Net Designer-2 (For Feed Back Type Network) 

·        Interactive and user friendly window

·        16K neurons and 1 million connections

·        0.1 million connections per second while using 486 based PC.

·        Maximum image size (128x128)

·        Random connectivity

·        Auto network building with optimized connections

·        Recall with noisy, offsetted and tilted images

·        Recall response 2.5 sec. in 486 based PC

·        Data generation and import of images from other files 

7.3.3     Neural Net Designer-3 (For Unsupervised Learning) 

·        Interactive and user friendly window

·        Supports most features of Multi Layered NN

·        Mixed mode operations for supervised and unsupervised learning

·        Network view

·        Probing of hidden neuron outputs

·        Data generation 

Feed Forward type multilayered Neural Networks are very popular for their generalization and feature extraction property. However the Feed Forward type network need supervised learning to train the network initially. Self-organizing networks on the other hand are used in application of image classification, speech recognition, language translation, etc. An algorithm is developed to train multilayered Feed Forward type network in both supervised and unsupervised mode. Unsupervised learning is achieved by enhancing the maximum output and de clustering the crowded classes simultaneously. Proposed algorithm allows to force any output to learn a desired class using supervised training like Back Propagation. The network uses multilayered architecture and hence it classifies the features. Population of each class could be controlled with greater flexibility.

There are various new concepts incorporated in the “Neural Net Designer” systems. There are capabilities of random connectivity, time delay neurons, use of complex neuron activation function etc. Among these the most useful feature of the system is network pruning. The following section describes the pruning algorithm used in our system. 

7.4       Proposed Algorithm for Pruning 

Configuration of optimal network for an input and output data set depends on the type of neurons selected in hidden layer. We still do not have a method to select appropriate type of neuron for a problem. However, the algorithm optimizes the network by selecting most appropriate type of neurons available in the network and their interconnections. Following are different steps of the optimization. 

Step 1:            Choose a multilayered network, which is already trained with desired input output data sets and has output error well below the desired value Emax.

Step 2:            Train the net, for a single pass with complete training using back propagation algorithm.

Step 3:            Reduce magnitude of all connections using Wij = Wij * nf where nf is forgetting coefficient, less than but close to 1.0.

Step 4:            Repeat the step 2 and 3 till total error minimizes well below desired limit Emax.

Step 5:            use successive approximation method as shown in the flow chart of figure 4 to remove the connection till error is > Emax. Sort the connections for every pass when the connections are removed.

Step 6:            Remove all neuron with no input connection or no output connections.

Step 7:            Neurons having single input or single output are removed and connections are reorganized appropriately.

Step 8:            If step 7 is applicable then train the network again. 

7.5       Results 

The above algorithm is tested with a fully connected multilayer neural network having more than one independent input-output function. For example we consider a network having inputs A, B, C, D and outputs P and Q such that P = A xor B and Q = C xor D. 

To solve given problem, a fully connected network is configured with four hidden neurons h1, h2, h3, and h4. After optimization the networks corresponding P and Q are isolated from each other. Also two hidden neurons h3 and h4 are eliminated (see fig – 5). In the second case, a two-dimensional image-mapping problem is examined. A network is configured initially with two analog inputs, thirteen hidden neurons in a single layer and an output neuron with binary output. Twelve hidden neurons input are of the form –  

Xj = ∑ (Wij * Yi) and Yj = 1 / (1 + ex) …..(1) 

Only one hidden neuron input is used with special summing function – 

Xj = ∑i (Wij * Yi2) and Yj = 1 / (1 + ex)…….(2) 

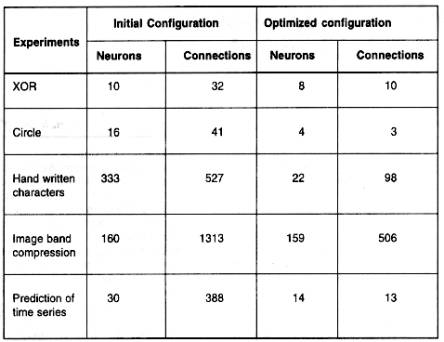
The network is trained to map a circle and then the network is optimized using above technique. Optimization result is shown in figure 6. The resultant network has only one hidden neuron and three connections. The neuron ‘selected’ by the optimization is the one, which is specially implanted in the network to solve the problem of circular boundary. Each of the above experiment is conducted ten times, and the results are shown in table 1. The above optimization algorithm is used in several other applications like (a) mapping of handwritten characters, (b) prediction of time series functions (c) complex Boolean functions and (d) image band compression etc. 

7.6       Conclusion 

Optimization of multi layer neural network is achieved by removing weakest connections from the network. Optimization of network has following advantages. 

1.      Reduces network size to minimum by optimizing the use of neurons and connections.

2.      Possibility of VLSI design

3.      Isolation of independent variable

4.      Easy to realize internal representation.

 Using above technique it is possible to design run time auto configuration of the network topology. 

7.7       References 

1.      Lippman R. P., An introduction to computing with neural nets. IEEE ASSP Magazine pp 4-22, April 1987.

2.      D.E. Rumalhert and J.L. McClelland, Parallel Distributed Processing Explorations in the Micro structure of cognition. Cambridge MA:MIT press, vol 1, 1986.

3.      R. Hetcht-Nielsen, “Theory of the back propagation neural network”, In Proc. Int. Joint. Conf. Neural Networks, vol 1. pp-593-611. New York: IEEE press, June 1989.

4.      E. D. Karnin “A Simple procedure for pruning back propagation trained neural network”, IEEE Trans, Neural Networks Vol. 1, pp 239-244, June 1990.

 

 

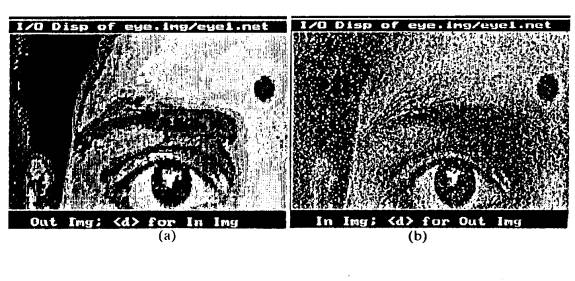
Fig 1 – Image band compression using 64-12-8-64 FFNN with 8x8 image window.
(a) is the output image corresponding to (b) 256x256x16 noisy gray image.

Fig 2 – Network optimization using “Neural Network Tool Box –1”. Figure (a) & (b) are FFNN to solve XOR problem before and after optimization respectively.


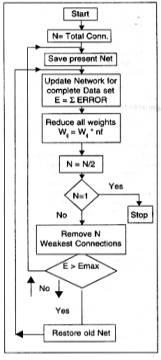
Fig 4 – Network Optimizing Algorithm, where Emax is the maximum tolerable error.

Fig 3- Time series prediction using Delay neuron in FFNN. (a) Complex periodic waveform (top trace) is predicted (bottom traces) along with expected output. (b) Shows 55 years sunspot activity by time delay FFNN.

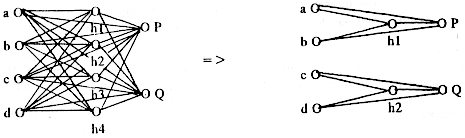
Figure 5 – Configuration of network before and after optimization. The above network is trained for P = A xor B and Q = C xor D. Optimized network on the right has split in two parts isolating two independent problems P and Q.

Fig 6 – In above example let R = ((X + 0.5) 2 + (Y - 0.5) 2) 0.5 and if (R < 0.3) then COL = 0 else COL = 1. X and Y are random analog inputs between 0 and 1. A special neuron S (See text) is implanted among the hidden neurons. In the network on the left. On the right is the optimized network where all the hidden neurons are replaced by a single special neuron S.

Table 1 – Results of network optimization for different types of input outputs. Optimized configuration presented here are average of ten experiments each started with different initial weights.

 

7.8  Published 

Himanshu S. Mazumdar  & Leena P. Rawal,  "A Neural Network Tool Box using C++", in CSI Communications, April, pp. 22-25, Bombay, 1995. Himanshu S. Mazumdar & Leena P. Rawal,  "A Neural Network Tool Box using C++ ", in CSI Communications, August, pp. 15-23, Bombay, 1995.(This paper has received "Best Article of the Month Award")