| RENT A THINKER |
|
|
|||||
| Home | My Page | Chat | Tik-Tok | ||||
3.1
ABSTRACT
3.2
INTRODUCTION
3.3
GRAPHICS SIMULATION
3.3.1
Standing on feet
3.3.2
Algorithm for Standing
3.3.3
Walking Algorithm
3.4
RESULTS
3.5
CONCLUSION
3.6
FUTURE WORK
3.7
REFERENCES3.8
PUBLISHED
Multi layered neural networks are being
applied in various fields of automation. One such application is developed for
simulation of two legged Robot to
balance and walk using Neural Network based learning technique. Human limbs are
simulated and a skeleton of the
human body is designed using computer graphics. A rule based
Neural Network Algorithm is developed to motivate the skeleton to walk.
The motivation is created using a set
of rules and an error functions to achieve the set goals. Some of the goals are
like- keeping the Center of Gravity (CG)
under the feet, keeping the average
height of the CG constant, spending minimum energy, traveling in a given
direction etc.. Using this algorithm, the seven limb joints
of the skeleton
are updated and the limbs
are plotted iteratively to produce
an animation effect of walking. The
ROBOT model is only inputted with the destination
co-ordinates, the actual movements of the limbs are generated
automatically similar to human walking. The algorithm uses a technique similar
to the gradient descendent method to minimize the error. Such algorithm may be
applied to solve transportation problems in non-uniform space using multi legged
( wheel-less) vehicles.
The nature has not provided wheels to the biological systems, however the
most man made systems need wheels for transportation. Wheel preserves energy and
is more efficient, provided it works on an uniform surface. Biological systems
on the other hand can move on non-uniform surfaces.
The basic difference between biological and manmade system is that most of the
manmade transportation system
do not have sensory signal feed back with information processing
capabilities. In case of the
transportation of the biological system, the eyes acquire the image of the
environment, brain processes the image and computes the co-ordinate location,
where the next step should be directed. While doing so, brain consider many
aspects like -(a) To keep the body
in equilibrium by keeping the CG
under the feet, (b) minimum change
in the CG height to preserve the potential and kinetic energy, (c)
Considering above two
points, it calculates the maximum step size
based on the dimensions and the degree of freedom of the limbs, (d) the
expected position of the step depending on the information received through eyes
etc..
The brain continuously optimizes all the parameters based on
different constraints as described above to move the body to the desired
position. These processes are called walking, running, scrolling etc. and are
very advance compared to any of the man made machines. To implement walking in
wheel-less mobile systems- it is necessary to map the cinematic details to the
processing and control unit so that an integrated control strategy is worked out
in a multi limbed flexible systems for transportation. This type of control
strategies are applicable to Robots, cranes, earthmovers, vehicles for distant
planet etc.. This paper describes one such control strategy based on NN
approach.
A model of human skeleton is simulated in two dimensional
computer graphics. The simulation uses 10 limbs with proportionate length and
weight. An algorithm is described to move the model on an artificial
one-dimensional surface. The operation has several goals like keeping at least
one leg on the surface at all the time, moving the body to the desired direction
etc.. The goals are implemented using rule-based approach. The control signals
are calculated for each limb depending on its current relative position and the
desired goals. This is achieved iteratively by using an error function similar
to FFNN [Rumalhert]. The sensitivity of the total error is calculated with
respect to each limbs movement. The gradient descendent technique is used to
update the incremental position of all the limbs. The following section
describes the details of the walking algorithm and the simulation ‘C’
program. In the RESULTS section, some examples of behavior of the model are
shown with the plots of model’s walking on different surfaces.
In this simulation, we have consider following ten limbs of human body -
(a) neck (b) body (c) left arm1 (d) left arm2 (e) right arm1 (f) right arm2 (g)
right thighs (h) right leg (i) left
thighs and (j) left leg. The fingers palms and feet are not included in
the simulation; however, feet play an important role in balancing the body and
walking. It is interring to note
that some people can walk on two sticks. Our simulation is similar to this. Each
limb is considered as one dimensional line segment having length and weight
proportional to that of the average human limbs.
A database is created for all the limbs each record has following
details. Length, weight, absolute angle, maximum angle, minimum angle, driving
end co-ordinates and other end co-ordinates. The maximum and minimum angles are
having relative values and measured with respect to the limb where it is
connected. A second database is used for the joints, which defines the
connectivity of limbs with respect to each other.
The limbs are assembled at any time using above database. To place the
model on a solid surface, the lowest tip of the limb is made to touch the
surface by appropriately offsetting all the coordinates.
Initially all the absolute limb angles are initialized with random
values.
The model is made to stand on its leg like human beings by maneuvering
the position of the center of gravity. Center of Gravity (CG) of each limb is
individually calculated and then the resultant co-ordinates of CG are
calculated. To make the model stand, two constraints are imposed- (a) the
average height of the CG with respect to the ground surface should be maintained
and (b) the CG should be maintained between two feet. To achieve the above
constraints, an iterative algorithm is developed, that minimizes the error of
the CG. At the end of every iteration the limb angles are updated; limbs are
reassembled and displayed on graphics screen to produce animation effect. To
achieve the desire goal of CG constraints as described in section 2.1, there are
may be possibilities of limb positions, e.g. the model could be upside down
standing on its head and still achieve the desired CG position. There are other
constraints added to the system. Some of them are (a) at least one of the leg
should touch the ground surface at all the time, (b) no limb should go below
ground surface (c) conserve the energy and (d) conserve the time.
The algorithm is based on minimizing the error of the primary goals using
gradient descendent technique i.e use for training MLNN. The algorithm is
described below -
From a given position to the standing position, the model goes through a
nonlinear translation of all the co-ordinates. During the translation, the model
is restricted by the constraints like limiting angles, CG etc. The model works
against gravitational field using the mussel forces, which drives the limb
joints. To compute the locus of each limb, the error sensitivity of each limb is
calculated. Depending on the magnetized and direction of these parameters, the
limbs are moved proportionally. The movement is made proportional to an
arbitrary constant ‘eta’, whose value is kept between 0.01 to 0.1. The
sensitivity is calculated by calculating moving the limbs by a small angle in
the direction and direction and have magnitudes as computed by the previous
iteration.
In section 2.2, we have seen that how the model can stand on its feet
from an arbitrary position. To make the robot walk, the model is given
additional constraints to reach a given co-ordinates in standing posture. These
constraints are (a) minimizing the
distance between the CG and the target location, (b) not dragging the body on
the floor surface (c) keeping at least one feet on the ground surface.
The simulated model is tested in different environment. The model is
brought to a random posture by choosing all the limb angles as random values and
then letting a model to stand on its own and walk. The several frames are drawn
between any two steps. each frame is drawn on alternate frame of the graphics.
The pages are switched so that the drawing and display are pipelined to increase
the display time.

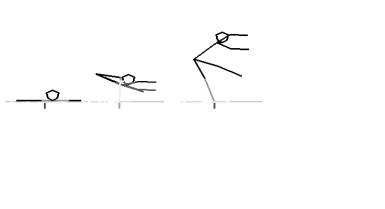
[Figure – 1(a)]
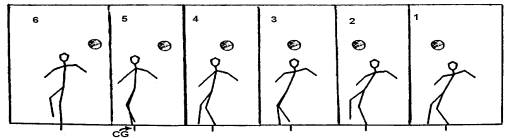
[Figure – 1(b)]
Figure-1 shows the capture picture of several frames from initial
random position to walking. The
small vertical line below the surface represents the CG of each position.
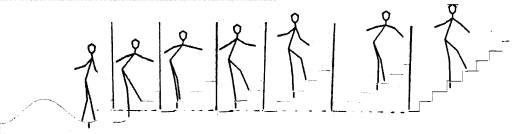
Figure -2 shows the model climbing to the staircase.

In figure - 3, the model is tested on a irregular surface.
In all the experiments, the simulation shows case similarity of the model
movement and human walking.
A computer graphics simulation of a human skeleton is made to perform
walking by balancing the limbs and CG. The walking algorithm is based on
gradient descendent technique. A neural network is trained with its inputs as
the current angles of the limb and the direction of movements. The output of the
network is trained with the next state of the corresponding angles. The network
is trained using the data from the above model.
It is possible to use the above algorithm for animation and automation in
making of cartoon films.
[1] William B. Gevarter, “
Intalligent Machines” ; an introductory perspective of Artificial
Intelligence and Robotics
[2] Ernest W. Kent, “ The Brains
of Men and Machines “, BYTE-McGrow Hill.
[3] Michael A. Arbib, “ The
Metaphorical Brain “, an
introduction to cybernetics as Artificial Intelligence and Brain theory
Mazumdar Himanshu. S., and Leena P. "A
novel algorithm for simulation of a (Two legged)
Robot using
Neural Network",
CSI Communications, ISSN 0970-647X, pp. 18-20, August, 1996.