| RENT A THINKER |
|
|
|||||
| Home | My Page | Chat | Tik-Tok | ||||
1.1
ABSTRACT
1.2
INTRODUCTION
1.3
LEARNING ALGORITHM
1.4
RESULTS
1.5
CONCLUSION
1.6
LISTING
1.7
REFERENCES
Single layer feed forward type networks are used for linear decision boundary [1]. To get solution of non-linear boundary, at least two layer networks are required [2]. In this paper, single layer topology is developed with appropriate learning algorithm to solve non-linear problem like XOR or circular decision boundary problems. Method used in this new topology is multivalued neuron activation function.
Frank
Rossenbatt invented the first meaningful adaptive architecture, i.e. “the
Perceptron” in 1957 [3]. The perceptron was actually an entire class of
architectures, composed of processing units that transmitted signals and adapted
their interconnection weights. It was oriented towards modeling the brain in an
attempt to understand memory, learning, and cognitive processes. But the crucial
limitation of the perceptron is that “it does not allow more than one layer of
adaptive weights”. Because there was no way to propagating the weights
correction through a multi-layer network in order to make such a network learn.
Afterwards, this limitation was overcome in 1986, by Rumalhart and Mcclelland by
presenting “ Back error Propagation Algorithm “[2]. The main functional
limitation of the perceptron is that an output unit can classify only “
linearly separable patterns”. The XOR function is classic example of a pattern
classification problem that is not linearly separable. To solve XOR problem, a
back error-propagating network is trained. The perceptron model is unable to
solve XOR problem with a single output unit because the function is not linearly
separable and its solution requires at least two layers network.
Here
in the paper, attempt has been made to get solution for XOR problem using single
layer neural network with a multivalued neuron activation function – Zo = f
(abs (Zi) + K). Choice of similar activation functions with appropriate learning
algorithm [3] for other non-linear problem minimizes the network topology
drastically resulting increasing the speed.
In
this section, the application of more complex activation function is shown to
solve non-linear boundary problem using single layer network.
The attempt also has been made to generalize the learning algorithm for
such application.
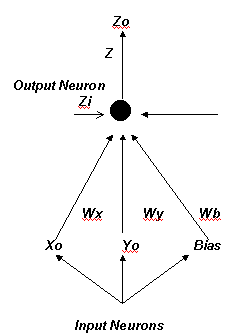
Let
us consider the below figure-1. with the replaced
activation function as-

Figure–1 The proposed network to solve the XOR problem
Zo
= ¦
( abs ( Zi ) + K ) (1)
where K is a constant
Here
¦(x)
is a threshold function of the type - if ( f(x) > 0 ) Zo = 1; else Zo =0;
With
this activation function we need to modify the training algorithm to reinforce
weights. Here, to calculate the error sensitivity of weights, we consider the
activation function as,
Consider
Zi = wx * xo + wy * yo + wb
(2)
Output
Zo = Zi 2 + K
Error
function E = ½ *( Zo - Zd )2
The
error sensitivity of wx is given by -
d
E / d
wx =
2 * (Zo-Zi)*
Zi * Xo
(3)
From
the above derivation, reinforcement of all the weights are -
wx = wx - h * ( Zo-Zd) * Zi * Xo,
Similarly,
wy = wy - h * ( Zo-Zd) * Zi * Yo
wb
= wb
- h
* ( Zo-Zd) * Zi
(4)
where
h
is the learning coefficient and is
generally varies between 0 to 1
The
table - 1 shows the result of 10 experiments with different initial weights to solve XOR problem. In this case the
constant K = 10 and minimum iterations = 30.
In all cases, the error becomes zero.
|
Experiment Type - XOR, K = 10 and eta = 0.4 |
||||
| Exp No. | wx | wy | Wb | Error / Iteration |
| 1 | 47107.027344 | -39776.375000 | 3773.969482 | 0 / 06 |
| 2 | -46319.484375 | 39967.570312 | 6637.256348 | 0 / 11 |
| 3 | 28691.703125 | -44370.238281 | 8611.723633 | 0 / 07 |
| 4 | 46208.574219 | -41672.371094 | 6987.809082 | 0 / 10 |
| 5 | 32130.199219 | -58266.539062 | 11717.017578 | 0 / 06 |
| 6 | -53111.601562 | 31523.916016 | 16880.552734 | 0 / 10 |
| 7 | -27263.140625 | -17786.228516 | -27561.998047 | 0 / 07 |
| 8 | 36554.726562 | -35102.531250 | -1199.843628 | 0 / 06 |
| 9 | -29898.927734 | 52755.171875 | -9632.140625 | 0 / 09 |
| 10 | 40373.308594 | -49587.156250 | 7200.447266 | 0 / 08 |
| Table - 3 The weights and output error for 10 experiments for “ XOR “ Problem | ||||
In
this section, it is observed that non-linear problems can not be solved using
single layer network with conventional type of neuron activation function. It is
shown that certain class of non-linear problems could be solved using more
complex neurons activation function much smaller having less complex network. Using
single layer network. Also it should be noted that the forward characteristics
of the network could be simplified without affecting the training performance by
using different activation function for forward and reverse characteristics.
It
is important to note that the backward activation function need not be the
gradient of forward activation function. e.g. we have chosen Zo= f(abs(Zi) + K)
as forward activation function where as for
the backward error propagation, Zo=Zi2 + K is used. This
increases the speed of forward computation. In general, the forward and the
reverse activation functions should have similar shape.
//Single Layer Neural Network Solution for XOR Problem
//By Himanshu
Mazumdar and
Dr. Leena H. Bhatt
//Physical Research Laboratory, Navrangpura, Ahmedabad - 380 009
//Configured with 2 inputs, 1 output
and 3 connections
//Date: - 23-February-2000.
#include
"stdio.h"
#include "math.h"
#include "graphics.h"
#include "conio.h"
#include "stdlib.h"
#include "time.h"
#define
OR 1;
#define
AND 2;
#define
XOR 3;
int
x1,y1,x2,y2;
float
wx,wy,wb;
float
m10,m12;
float
eta=0.4;
unsigned
int tx[5000],ty[5000],td[5000];
/*_________________________________*/
int update(int x0, int y0, float *zi)
{
int zo;
*zi=wx*x0+wy*y0+wb;
zo=fabs(*zi)+10;
if (zo>0) zo=0; else zo=1;
return(zo);
}
/*_________________________________*/
int reinforce(int x0, int y0, int zd)
{
int err,zo;
float zi;
zo=update(x0,y0,&zi);
err=zo-zd;
wx=wx-eta*err*zi*x0;
wy=wy-eta*err*zi*y0;
wb=wb-eta*err*zi;
return(err);
}
/*_________________________________*/
int train(int nmax)
{
int n,e,err=0;
int x0,y0,zd;
static int m=0;
for(n=0;n<nmax;n++){
x0=tx[m];
y0=ty[m];
zd=td[m];
e=reinforce(x0,y0,zd);
err=err+abs(e);
m++;
m=m% 5000;
}
return(err);
}
/*_________________________________*/
void desiredout(int smax)
{
int n,x0,y0,zd;
for(n=0;n<smax;n++){
x0=random(2);
y0=random(2);
/* XOR */
zd=x0 ^ y0;
tx[n]=x0;
ty[n]=y0;
td[n]=zd;
}
}
/*_________________________________*/
void initweights (void)
{
wx=1.0-random(1000)/500.0;
wy=1.0-random(1000)/500.0;
wb=1.0-random(1000)/500.0;
}
/*_________________________________*/
void main(void)
{
int
m,r,err;
clrscr();
printf("\n\n\n");
printf("*********************************************\n");
printf("*
Single Layer Neural Network
*\n");
printf("*
Solution for XOR Problem
*\n");
printf("*
by
*\n");
printf("* Himanshu Mazumdar
*\n");
printf("*
and
*\n");
printf("* Dr.
Lina Rawal
*\n");
printf("*
Physical Research Laboratory,
* \n");
printf("*
Navrangpura, Ahmedabad - 380 009
* \n");
printf("*
Configured with 2 inputs, 1 output
* \n");
printf("*
and 3 connections
* \n");
printf("*
Date:- 3-April-1996
* \n");
printf("*********************************************\n");
getch();
randomize();
clrscr();
printf("\n
Single layer solution for XOR problem
");
printf("\n
--------------------------------------
");
printf("\t\n\nExp no.
wx
wy
wb
");
printf("\n ");
initweights();
desiredout(5000);
for(r=1;r<=10;r++)
{
for(m=1;m<=700;m++){
err=train(16);
//printf("\n%d Error=%d",m,err);
if(err==0)break;
//getch();
}
printf("\t\t\t\n%d \t %f
%f %f",r,wx,wy,wb);
initweights();
}
getch();
printf("\n\nThe weights and output error for XOR problem" );
getch();
}
/*_________________________________*/
[1]
Judith E. Dayhoff, “ Neural Network architectures ”, An introduction,
ISBN-0-442-20 744-1.
[2] Rumalhert D. E, and L. McClelland, 1986,” Parallel Distributing
Processing, vol.1 and 2,Cambrige,
Mass: MIT press.
[3] Himanshu Mazumdar and Leena Rawal, “ A Neural Network Tool Box Using
C++.” CSI (Computer Society of India) Communications, April (22 - 27),
1997, INDIA
Published:
Mazumdar Himanshu. S., and Leena P. "Single
Layer Neural Network Solution for XOR Problem",
CSI Communications, ISSN
0970 – 647X, pp. 13-15, October,
2000.